Did We Invent It Or Did We Discover It?

You know what I am talking about.

Nov 11, 2024

I’ve been noodling this one in the hopper for a while, time to let it break free.

At first blush, this might seem to be about maths1 and it certainly connects, but it’s really about those who challenge the status quo, see something different, push boundaries, which, not coincidentally is exactly what great startups do. (More on that in the follow up edition.)

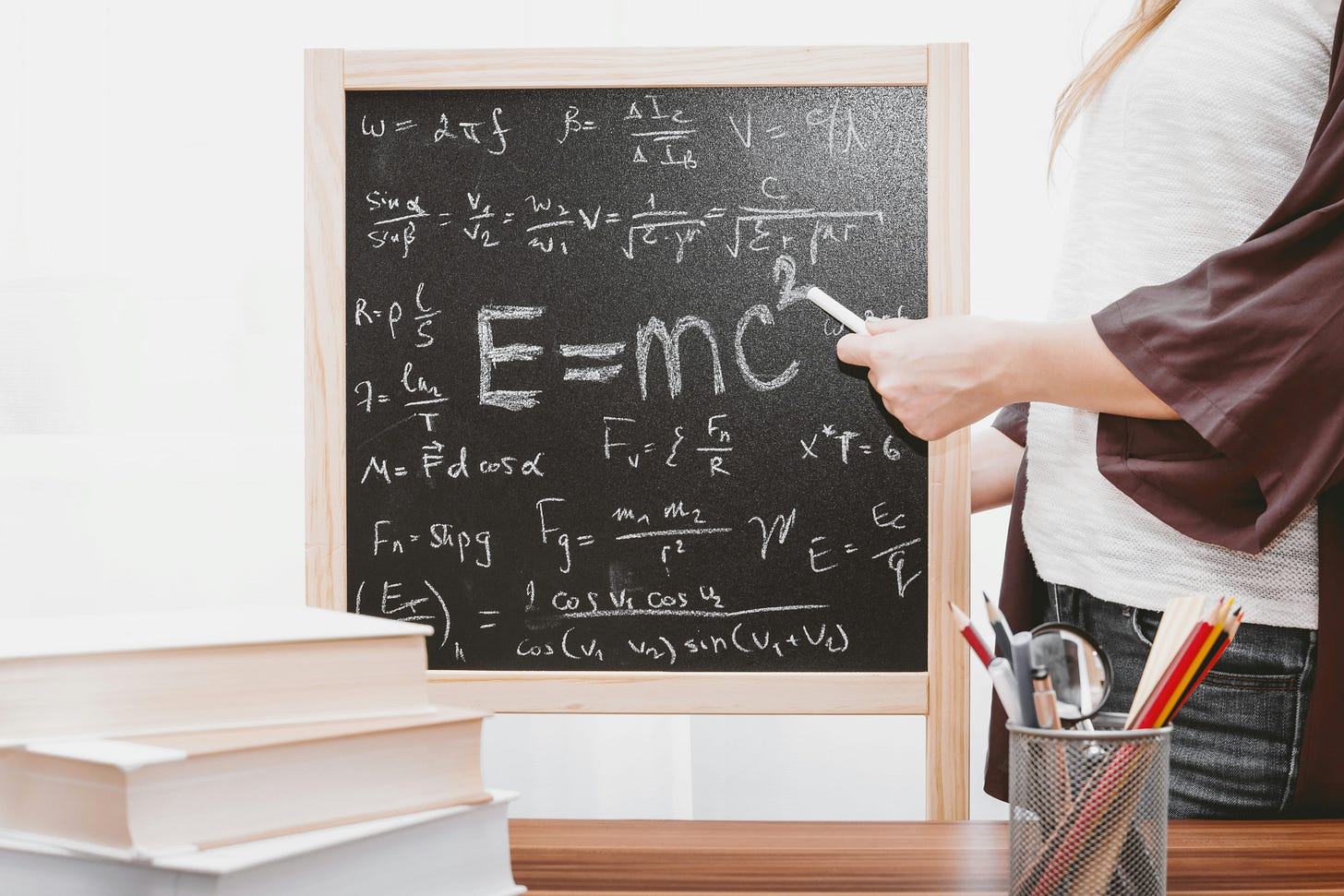
The maths isn’t hard. The idea is to do a spot of cloud hopping. (Plucking a piece of thinking from one discipline and applying it to another.) Why maths? Because.2

The question of whether maths is a natural phenomenon waiting to be discovered or a human invention is a debate that likely got started about a nano second after someone came up with ‘counting’.

The question will be phrased something like;

Is mathematics a universal truth that exists independently of humanity, or is it a conceptual framework we’ve created to make sense of the world?

Yup, as Ms. Vito said - it’s a trick question.

Not for the complex reason that she unpacks in the clip above. It’s a trick question because the question ‘OR’ … leaves no room for the actual answer … ‘AND’.

Mathematics is both invented AND discovered - and that isn’t a cop out - its …

When in my teens, my teacher said …

If everything we knew about maths - everything - was contained in this room you are sitting in and there in the corner of the room is a small 1 inch cube (this was before ‘we went metric’), that 1 inch cube would contain all the maths that can be applied to the world we understand today.

🤯 .. you can see why I got into this stuff can’t you?

All this was before I decided to study ‘double maths and physics’ for what were called ‘A’ Levels in England in those days. ‘Double Maths’, being a study on the one hand ‘Pure’ Maths while on the other, ‘Applied’ Maths.

This separation is important, because I think it lies at the crux of the question.

And just ‘for the record’ - my personal ‘favorite’ is ‘Pure Maths’.

Take something as basic as 1 + 1. “That’s 2,” most people would say, and they’d be right. But then there are times when I would argue that “it’s 10.” Both answers are spot-on, depending on the rules you’re playing by. In base 10 (our usual way of counting), 1 + 1 is 2. But in base 2 (binary), it’s 10. We live in a world built on assumptions, and one of those is that maths operates in base 10. Change that assumption, and you’re not just counting differently—you’re rethinking the world.

And with the scene set, let us explore with a view to answering the essential question … Are Mathematicians Explorers or Inventors?

The Inventors

The maths we learn is a language, a language people created and it’s full of numbers, symbols, and rules that all goes someway to making sense of our world.

Think about it:

• The number “5”? ‘We’ came up with that. (The Roman’s used ‘V’.)

• The infinity symbol (∞)? Pure human invention.

• That little ‘i’ for imaginary numbers? Yeah, we made that up too.

Over time we have combined these symbols and then built and applied rules to create mathematical images of the underlying logic. And all of this sits very much in invention (the domain of the Pure Mathematicians). It’s that room full of Maths that I talked about earlier.

And one more thought. There isn’t a single language of maths. There are many. Some radically different, some are just a different way of looking at a problem. None of them are ‘wrong’.

The Explorers

Meanwhile, in ‘Applied Maths’ land, people are attempting to understand the world around them. And then beyond understanding, postulating principles and rules of how our world behaves, so we can better understand it.

And then we try to break that rule - with ‘ah ha moments’! As we seem to get closer and closer to ‘the truth’ of out world. Sometimes it takes a long time to break the rule.

Case in point - Newton came up with gravity, or to be specific - discovered gravity - because let’s face it, we were all firmly attached to the world before Newton. Nobody was floating off into space. What Newton did was find a mathematical way of describing how Gravity works ..

.. and then tried to break it. So did others. They couldn’t and so it became one of those irrefutable things that holds - until it didn’t.

That’s kind of what Einstein did a little over 200 years later. And a hundred years after that we are still trying to wrap our heads around what Albert did. (Other than breaking what we all thought was a rule), because Einstein clearly demonstrated that Newton’s laws don’t hold up in certain situations. He also provided a very thorough summary what he thought would happen in those changed conditions.

That’s the interesting bit about Applied Maths, once we’ve invented these mathematical ‘words describing worlds’, we start stumbling upon truths about the universe that were always there, just waiting for us to notice. But for us to notice, it has to be seen in the context of the time. It’s no surprise that Isaac didn’t think about the Quantum realm when he was coming up with his laws and equally unsurprising that Albert did!

The ‘maths’ is invented. The stuff it describes is discovered, but discovery only happens when you ‘go there’. And to go there - you kind of need to know it’s there to go to.

Is Maths Invented or Discovered - image generated by ChatGPT

Sometimes what is being described is easy to get your head around - when it gets to multi dimensional universes - well, people who know what they are doing can visualize those universes by reading the maths. If you can’t read maths - the visualization is a lot harder. (To compare, think of reading a musical score and hearing it all in your head - few can do that - we need the orchestra - but those that can in the world of music are like those multi-dimensional mathematicians.

So Let’s Simplify. How About Triangles?

We all (kind of) know this one right?

In any right angle triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of squares of the lengths of the other two sides.

That entire paragraph can be written as ‘a² + b² = c²’, how cool is that?

The point is that long before people walked on planet earth, this was a universal truth. It was there as a truth for millennia (and no - I wasn’t there despite what my daughter might think), but I think it’s a safe bet that not many people thought too much about it. Until one day they did. For the sake of argument - let’s call him Pythagoras. (It’s an argument because we don’t really know who first thought about the problem - we just know it was Pythagoras that proved it.)

In other words - just like today - an observation was explored and people conjectured and there will have been all kinds of discussions until one day, this dude from Samos definitively proves it and it becomes known as ‘Pythagoras’ Theorem’.

And it’s absolutely foundational to Euclidean geometry.

Wait. What now? Euclidean Geometry? Aaah yes, sorry - new term.

Euclid wandered around the earth a couple of hundred years after Pythagoras and to keep the story simple, he essentially collected all that was known about geometry and came up with a set of rules that universally worked in describing ‘geometry’ and associated equations.

All was good though pretty quickly some pesky people started questioning the ‘TRUTH’ of Euclidean Geometry.

If memory serves a few hundred years went by as this new branch of maths got developed under the name Spherical Geometry. - and just as it started to settle - hell fire - people only started talking about Hyperbolic Geometry - and no need to worry, I am not going to dive into that nest - except to say that in the early 1800s some mathematicians started to seriously to get down to it, including a Russian Mathematician by name of Nikolai Lobachevsky.

My best and highly uneducated and certainly un-researched estimate as to how many people recognize the name ‘Nikloai Lobachevsky’ would be low. Very, very low.

AND if you have heard of him, the chances are that you don’t associate him with being the founding father of something called Hyperbolic Geometry, but rather a song written and performed here by the mathematician Tom Lehrer in 1960.

Seriously - don’t jump over it. Very clever. Very funny. Well worth a listen.

You knew I’d have to get a song in here somehow - didn’t you?

OK - back to the plot. What’s all this to do with the topic at hand?

Answer? Everything.

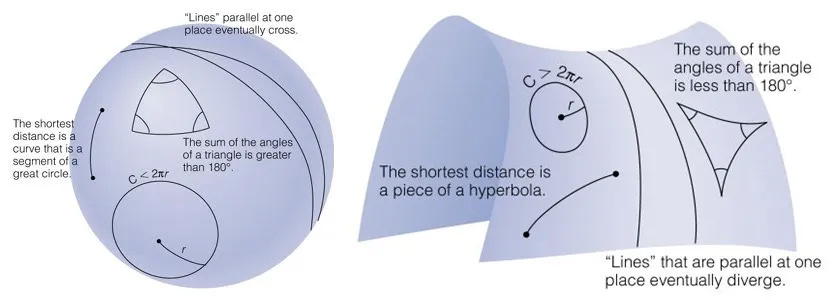
Pythagoras and Euclid did a great job of describing a flat world. BUT - when others started to think of non flat objects and applied those equations - things start breaking. in fact all hell breaks loose. Just try drawing a big triangle on the surface of a sphere and then add up the three angles. In Euclidean geometry adding the three angles together of ANY triangle gives you an answer of 180.

On a sphere, not only is the total always greater than 180, the total varies. Needless to say this kind of messes things up.

A good PURE mathematician is exactly this kind of person. They like to look at something that is a known irrefutable fact - and then refute it.

Take our man Nicolai. It all started when he decided to challenge Euclid's fifth postulate, which basically said “only one parallel line can be drawn through a point not on a given line”.

Seems reasonable. Even as I read it, I nod my head and agree. Yup - pretty much a foundational concept.

Lobachevsky asked whether it was possible to draw more than one line through a point that is parallel to a given line. 🤯 .. you see what I mean about these dudes. Why would you even start to think that way?

Lobachevsky was inventing by not sticking with ‘common wisdom’. Out of that line of thought emerged everything that we today call Hyperbolic Geometry. Yes, but really? What use is that?

Answer in full at Geeks for Geeks, but some quick bullets to start you off …

Google Maps and Navigation
Gravity and Special Relativity
Computer Graphics and Visualization
Physics and Cosmology
Architecture and Urban Planning
Art and Design
Mathematics Education and Research

.. if there was no hyperbolic geometry - we would miss out on a lot of stuff!

Here’s The Thing

Sometimes, when we invent new maths to solve a problem, we stumble onto an entire hidden reality we didn’t even know existed.

‘Complex numbers’ is another example. We cooked them up to deal with equations that didn’t play nice with the usual rules, but they turned out to be key to understanding things like electricity and quantum mechanics.

Without ‘i’ you wouldn’t using a phone/computer/tablet to read this newsletter.

BUT - if we hadn’t adopted the Arabic numbering system and stuck with Roman Numerals - would we have even been able to unpack what we have achieved?

The Ever-Changing Language of Maths

When I was a kid we didn’t have ‘selfies’. Now we do. Things evolve. Language evolves. Maths is a language. Maths evolves, We add new terms to describe new ideas, solve new problems, or just bring a little order to the chaos. From calculus to cryptography, math isn’t some dusty relic; it’s a living, evolving language, shaped by human curiosity and a stubborn need to understand.

Maths is beautiful - because what it describes is beautiful, like this image …

I’m not going to explain it. Mainly because I don’t understand it. What I can tell you is that the man behind it lives on Maui, surfs a great deal and operates outside of mainstream thinking in US Universities.

You will have heard of something called String Theory. My man from Maui says that String Theory is wrong. (Ballsy when you think about it - since the vast majority of the people in the world that operate in this space are big supporters of same.) Garrett say no. Garret say ‘too complicated, nature doesn’t do complicated’.

Here’s the thing - nobody has yet disproved his theory and so far he hasn’t disproved String Theory. So there we have it. Two theories amongst a handful all trying to explain the world around us. We aren’t there yet. BUT all those theories utilize maths that we invented - to bottom out and describe the reality that we have thus far identified.

So. Am I right? Is It ‘AND’, not ‘OR’? Tell me what YOU think.

Human By Design

Discussion about this post